SEMESTER 1 BAB 1
1. Jika p bernilai Benar , q bernilai Benar dan r bernilai Salah
Tentukan nilai kebenaran dari \rightarrow r)
Pembahasan
3. Tentukan nilai x agar pernyataan majemuk berikut menjadi benar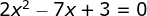 ,
,
x adalah bilangan real “
Pembahasan
Agar Implikasi bernilai benar , karena pernyataan 1 sudah bernilai benar maka
pernyataan 2 harus benar.
Pernyataan 2 benar bila x diisi bilangan yang tepat , yaitu :
4. Buatlah negasi dari
“ Ada ikan bernapas dengan paru-paru atau Semua
6. Buatlah Ingkaran dari pernyataan majemuk)
Pembahasan
7. Tunjukan apakah pernyataan majemuk
\vee r\textbf{}) ekuivalen dengan
ekuivalen dengan \rightarrow r)
Pembahasan
Pembahasan
Pembahasan
3. Tentukan nilai x agar pernyataan majemuk berikut menjadi benar
x adalah bilangan real “
Pembahasan
Agar Implikasi bernilai benar , karena pernyataan 1 sudah bernilai benar maka
pernyataan 2 harus benar.
Pernyataan 2 benar bila x diisi bilangan yang tepat , yaitu :
4. Buatlah negasi dari
“ Ada ikan bernapas dengan paru-paru atau Semua
ikan Bernapas dengan insang “ .
Pembahasan
Ingkaran atau negasi dari Disjungsi adalah
5. Tentukan Konvers , Invers dan
Kontraposisi dari :
“ Jika Semua pencuri masuk penjara maka Negara
aman “ .
Pembahasan
Konvers :
“ Jika Negara aman maka Semua pencuri masuk penjara “ .
“ Jika Negara aman maka Semua pencuri masuk penjara “ .
Invers :
“ Jika Ada pencuri tidak masuk penjara maka Negara tidak aman “ .
“ Jika Ada pencuri tidak masuk penjara maka Negara tidak aman “ .
Kontra Posisi :
“ Jika Negara tidak aman maka Ada pencuri tidak masuk penjara “ .
“ Jika Negara tidak aman maka Ada pencuri tidak masuk penjara “ .
6. Buatlah Ingkaran dari pernyataan majemuk
Pembahasan
7. Tunjukan apakah pernyataan majemuk
Pembahasan
8.
Diketahui pernyataan :
premis 1 : Jika hari panas maka Ani
memakai topi
premis 2 : Ani tidak memakai topi atau ia
memakai payung
premis 3 : Ani tidak memakai payung
Kesimpulan yang
sah dari ketiga premis diatas adalah ….
Pembahasan
9. Tentukan Ingkaran dari konvers \rightarrow \sim r)
Pembahasan
Dari implikasi dibuat konvers dulu, kemudian dari
)
kemudian dari konvers tersebut dibuat ingkarannya
) ekuivalen dengan
ekuivalen dengan 
sehingga jawabannya :
 \right )) ekuivalen dengan
ekuivalen dengan )
10. Tunjukan Sah tidaknya penarikan kesimpulan berikut
Pembahasan
Dari implikasi dibuat konvers dulu, kemudian dari
konvers
dibuat ingkaranya
Konvers dari
implikasi(soal) kemudian dari konvers tersebut dibuat ingkarannya
dengan
berpatokan ingkaran dari implikasi ,yaitu :
sehingga jawabannya :
10. Tunjukan Sah tidaknya penarikan kesimpulan berikut
Pembahasan
Nilai
kebenaran premis 1 dan premis 2 dihubungkan
dengan menggunakan
konjungsi,hasilnya dihubungka
dengan kesimpulan menggunakan
implikasi ,jika nilai
kebenaran semua benar (TAUTOLOGI)
penarika
kesimpulan
sah.
atau dengan
cara lain,yaitu premis 2 diganti dengan tanda
hubung implikasi yang mempunyai
nilai ekuivalen yaitu














